人工智慧-梯度下降法

學習機器學習常會看到這樣的圖1，看上去好複雜啊，這些和我們所說的梯度下降又有什麼關係呢?原來這些圖片展示出來了一個家族的歷史，這個家族的名字叫做Optimization(最佳化問題)，最佳化能力是人類史上的重大突破，它解決了很多實際生活中的問題。從而漸漸演化成為了一個龐大的家族，比如說: 牛頓法, Newton's method、最小平方法Least Squared Method、梯度下降法Gradient Descent等等...而我們神經網路就屬於梯度下降法這個分支當中的一個。因為這就是傳說中梯度下降裡面的梯度了Gradient。
                                                                                                     
                                                                                                                                                                                               圖1 梯度下降

初學神經網路的時候我們通常會遇到這樣的一個方程式，叫做誤差方程式(cost function)，用來計算預測出來的值和我們識別中的值有多大差別?在預測數值的問題當中我們常會用到平方差，Mean Squared Error來代替如(式1-1)。

                                                                                                                                                                        Cost = (predicted - real)²      (式1-1)
                                                                                                                                                                                                                                            = (Wx - y)²                      (式1-2)
                                                                                                                                                                                 = (W - 0)²                               (式1-3)

 

我們簡化一下這個方程式如(式1-2)，W是我們神經網路裡面的參數, x和y都是我們的數據。因為x和y都是實實在在的數據點，在這個假設中是多少都無所謂，然後我們像這樣再簡化一下如(式1-3)，注意! 這個過程在數學中並不正確，不過我們只是為了看效果，所以現在的誤差曲線就變成這樣如圖2，假設我們初始化的黑點W在這個位置，而這個位置的斜率就是虛線，這也就是梯度下降中的梯度了，我們從圖2中可以看出Cost誤差最小的時候，正是這條Cost曲線最低的地方，不過在黑點的W卻不知道這件事情，它目前所知道的就是梯度線為自己在這個位置上指出的一個下降方向，我們就要朝著這個黑色梯度虛線的方向下降一點點，再作一條切線，發現我還能繼續下降，那我就朝著梯度的方向再繼續下降，這時再展示出現在的梯度，因為梯度線已經躺平了，我們已經指不出哪邊是下降的方向了，所以這時候我們就找到了黑點W參數的最理想值，簡而言之就是找到梯度躺平的點(Global cost minimum)。

                                                                                                                            
                                                                                                                                                                                  圖2 簡化的梯度下降

可是神經網路的梯度下降可沒有這麼簡單，神經網路裡面的W可不只一個，如果只有一個W我們就可以畫出如圖2這樣的誤差曲線，如果只有兩個W也很簡單，我們可以使用一個3D的圖像來展示，可是超過3個W我們就沒有那麼好的辦法可辨視出來。在通常的神經網路中，誤差曲線可沒有這麼單純，在簡化版的誤差曲線中我們只要找到梯度線躺平的地方，就能迅速地找到誤差最小時的W(如圖2 Global cost minimum)。

                                                                                                                            
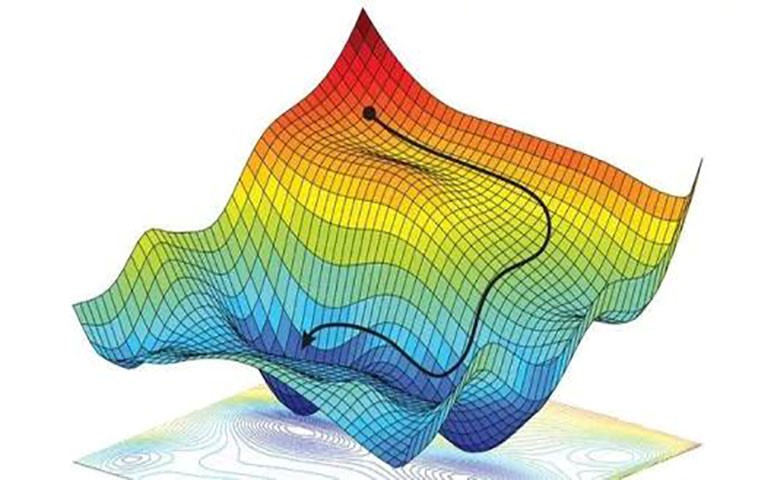
                                                                                                                                                                                 圖3 正常梯度下降法

可是很多情況是這樣的，誤差曲線並不只有一個最低點，而且梯度躺平的點也不只有一個，不同的W初始化的位置將會帶來不同的下降區域，不同的下降區域又會帶來不同W的解，在這個圖3當中, W的全局最佳解Global cost minimum在這個位置，而其他的解都是局部最佳(Local cost minimum)，Global cost minimum的解固然最好，但是很多時候你手中都是一個Local cost minimum，這是不可避免的，因為雖然不是Global cost minimun，但是神經網路也能讓你的local cost minimum足夠優秀，以致於即使拿這個Local cost minimum也能出色地完成手中的任務。