理解時域、頻域、FFT
傅立葉變換有助於理解常見的信號。儘管傅立葉轉換是一個複雜的數學函數,但是通過一個測量來理解傅立葉變換的概念並不複雜。從根本上說,傅立葉變換是將一個信號分解為不同振幅和頻率的正弦波。
時域
描述數學函數或物理信號對時間的關係。一個信號的時域波形可以表達信號隨著時間的變化。若考慮離散時間,時域中的函數或信號,在各個離散時間點的數值均為已知。若考慮連續時間,則函數或信號在任一時間的數值均為已知。在量測時域的信號時,常會用示波器將信號轉換為其時域的波形。
頻域
描述信號在頻率方面特性時用到的一種座標系。對一個信號來說,它有兩方面的特性,如信號強度隨時間的變化規律(時域特性),信號由哪些單一頻率的信號合成的(頻域特性)。
所有信號都是若干正弦波的和
通常把一個實際信號看作是根據時間變化的電壓值。這是從時域的角度來觀察信號。傅立葉定律指出,任意波形在時遇上都可以由若干個正弦波和餘弦波的加權和來表示。例如有兩個正弦波,其中一個的頻率是另一個的3倍。將兩個正弦波相加,就得到一個不同的信號。
假設第二個波形振幅也是第一個波形的1/3。此時只有波峰受影響。
假設加上一個振幅和頻率只有原信號1/5的信號。按照這種方式累加直到碰觸到Noise邊界,則信號會形成一方波。

使用FFT分解信號
傅立葉轉換將一個時域信號轉換為頻域信號。頻域信號顯示了不同頻率對應的電壓。頻域是另一種觀察信號的角度。查看圖1中的信號,有兩個頻率不同的信號。在該情況下,頻域中就會顯示兩條不同頻率的能量。

在頻域裡也可以觀察到信號的形狀。例如,頻域中方波信號的形狀。使用不同頻率的正弦波創建一個方波,即可預見在頻域中,這些信號都會被表示為一能量,每一能量都表示組成方波的正弦波。如頻域中,能量顯示為一個梯度就可知道原信號是一個方波信號。
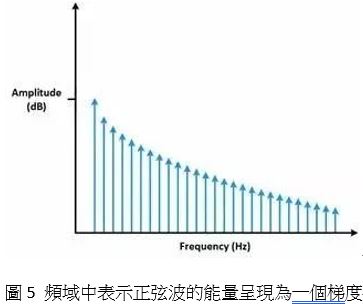
現實生活中,需多混合信號示波器(MSO)都有FFT功能。下圖中,可以觀察到信號途中,方波FFT是如何顯示的。放大後可觀察到頻域中的尖峰。
在頻域中觀察信號有助於驗證和發現信號中的問題。例如,假設有一個輸出正弦波的電路。可在示波器上查看時域信號,如圖7所示。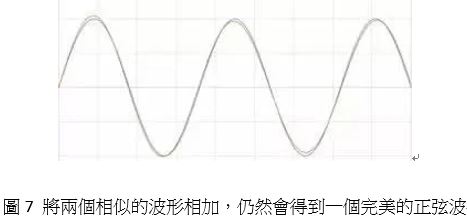
在頻域中查看信號時,如果輸出的正弦波頻率穩定,應該只在頻率中顯示為一能量。但是可以看到在更高的頻率上仍然有一能量,表示正弦波並不如觀察到的那麼完美。
頻譜分析
頻譜上以數學觀點來看可以分為正數頻譜與負數頻譜,其由來是將訊號以尤拉公式(Euler formula)改寫,以例子表示式如下: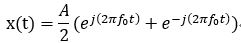
上式的意思為訊號振幅出現在正頻率及負頻率-點上以脈衝表示如圖9。但實際上沒有負數頻譜現象,我們所觀察到的頻譜都是以正數頻譜來表示如圖10。
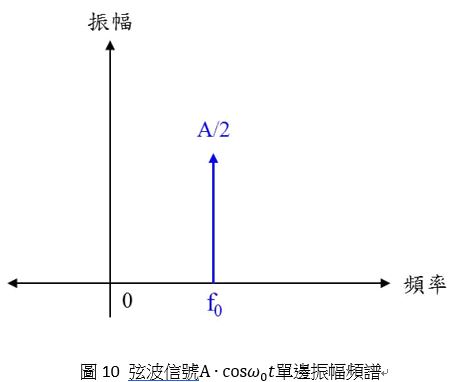
仔細觀察圖9、10可發現在頻譜上所觀察到的訊號強度為實際訊號的一半,因此可說明頻譜是以對稱方式來呈現且在正、負頻譜上各別分得訊號的一半振幅。
通常頻譜上是以能量(Energy)來表示,利用巴斯瓦定理(Parsevel’s theorem)來計算頻譜上訊號的能量,它是用來說明時域和頻域上運算的對等關係,公式如下:
接著以圖6為例列出其在頻譜上顯示的能量:
- 先列出方波在時域上的表示式 (僅考慮到5次諧波)
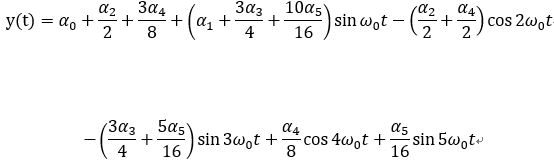
- 利用尤拉公式改寫
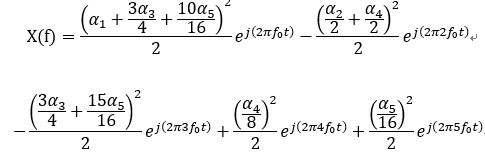
如下圖顯示出個頻率點的能量大小。
快速傅立葉轉換
執行快速傅立葉轉換時,將同調取樣定理(Coherent theorem)做正確的設定乃是相當重要的步驟,關係如下:
FS為取樣頻率、Ft為待測訊號頻率、N為取樣點數、M為待測訊號周期數,其中M、N必須為互質。同調取樣定理所表達的意義為取樣點數N必須在待測訊號周期數M內取完且所取的每一點在M個週期下的相同相位不可重複,如圖12所示。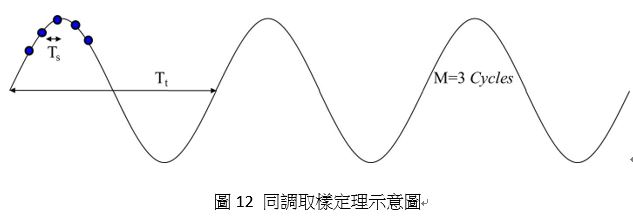
因快速傅立葉轉換是將測試訊號離散化,在以離散化之後的取樣點呈現原本連續的測試訊號執行轉換,如圖13所示。
假設取樣的資料完整的呈現原本連續的待測訊號,則頻譜上的信號能量與諧波能量將精準的顯示在此能量或諧波所在頻率,反之取樣的資料無法完整的呈現原本連續的待測訊號如圖14,那麼信號能量包含諧波能量將分散在此能量或諧波所在頻率的附近頻帶,如圖15所示稱為洩漏效應(Leakage effect),導致影響估算參數的準確度,但此洩漏效應可用同調取樣定理解決之,且估算之準確度又與取樣點數相關,取樣點數越多計算量越大準確度高;取樣點數越少則反之。
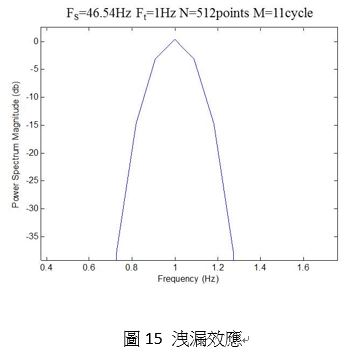
此外窗型函數也是影響準確度的參數之一,假設窗型函數未正確設定,則估算之頻譜能量未受到正確之補償,其估算功率洩漏的現象,將會影響其準確度。
信號加窗
使用FFT分析信號的頻率成分時,分析的是有限的數據集合。FFT認為波形是一組有限數據的集合,一個連續的波形是由若干小波形組成的。時間上,波形的前後兩個端點是相連的。如測量的信號是週期信號,採集時間內剛好有整數的週期,那麼FFT的上述假設合理。
可通過加窗來盡可能減少在非整數個週期上進行FFT產生的誤差。數位取樣到的有限序列的邊界會呈現不連續性。加窗可減少這些不連續部分的振幅。加窗包含將時間紀錄乘以有限長度的窗,窗的振幅逐漸變小,在邊沿處為0。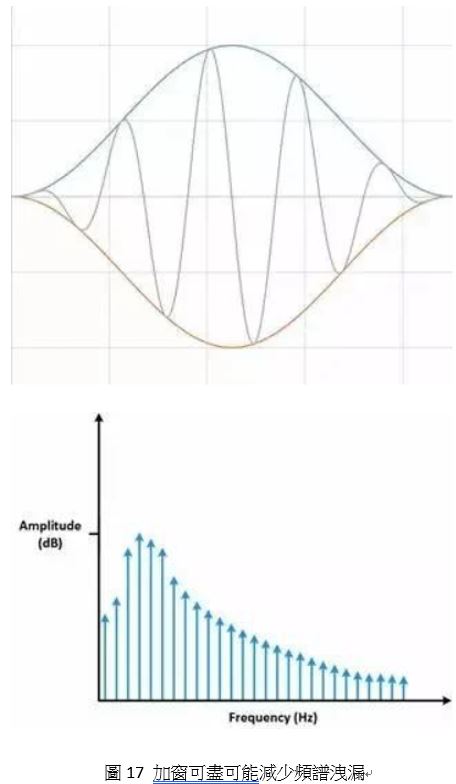
選擇加窗函數並非易事。每一種加窗函數都有其特徵和適用範圍。要選加窗和數,必須先估計信號的頻率成分。
Hanning窗用適於95%的情況。它不僅有較好的頻率解析度,還可減少頻譜洩漏。如不知道信號特徵但又想使用平滑窗,就選擇Hanning窗。
評論